Series 1: Stacks

What is a Stack? What does a Stack Trace Mean? Why is Stack so commonly used across all programming languages?

Do you like Potato chips ?

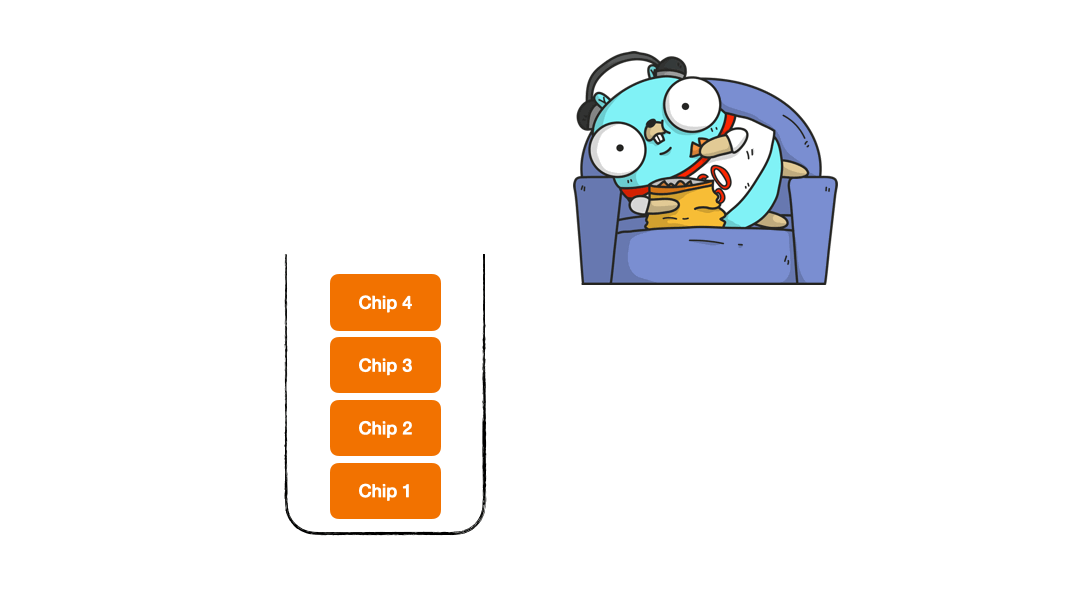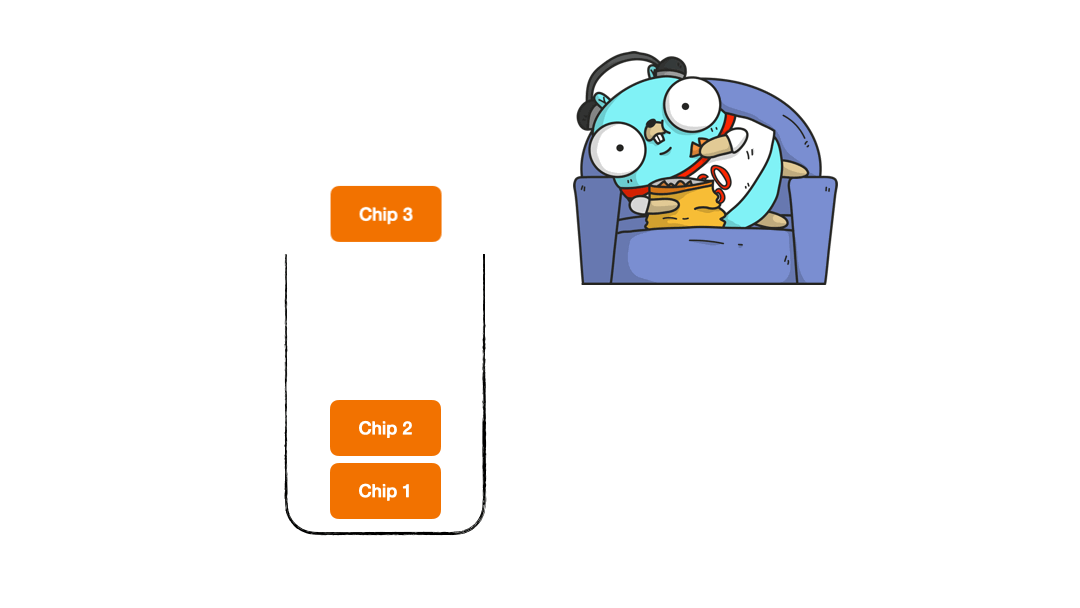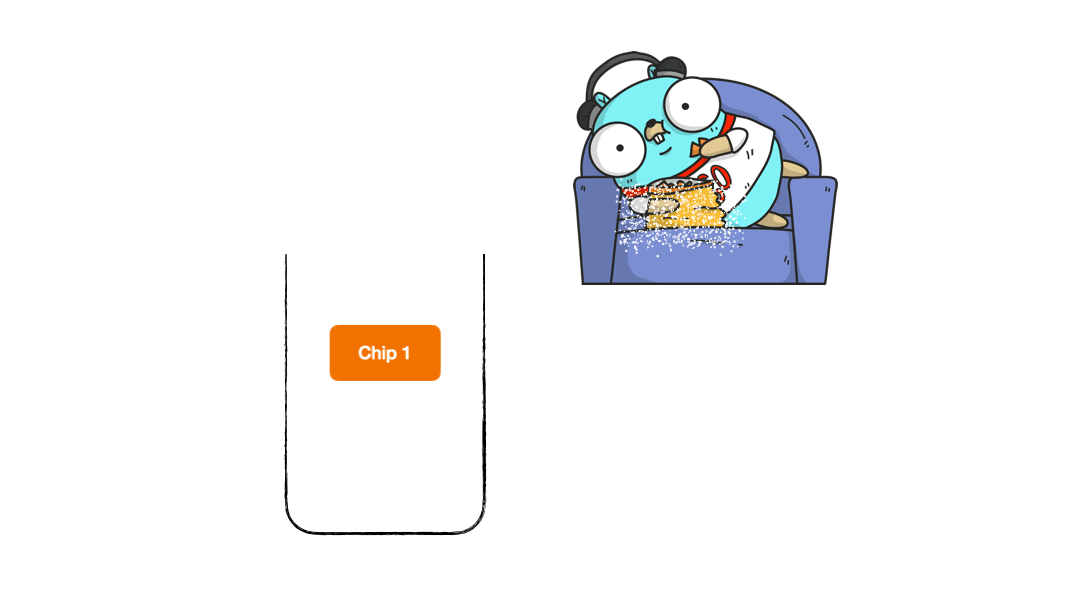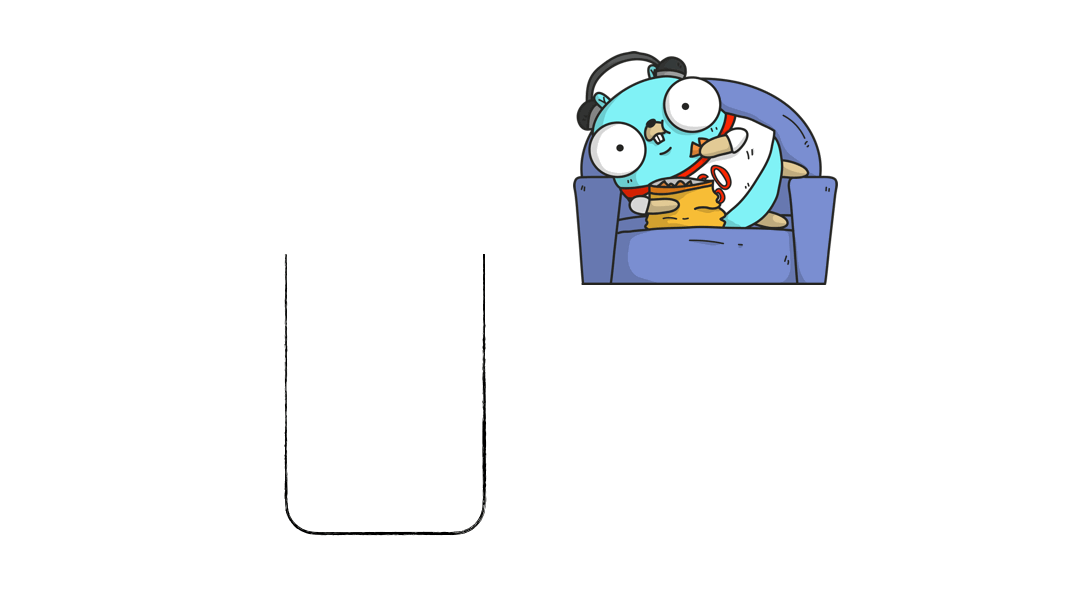
Notice something about this can? The chips are stacked vertically one above another. The only way to eat chips is to eat one from the top.

What goes inside first comes out last. This is also known as LIFO (Last In First Out) in computer science. The first chip that was added into the box is the last chip that we will eat.

What is definition of a Stack ?

A Stack is an abstract data structure which serves as a collection of elements on which any operation can only performed in the order LIFO (Last In First Out)

Keeping the above definition as a mental model, let's define some actions which are critical to this data structure.

There are 2 actions that are key to this concept:

Adding chips to the box - we name it as a PUSH operation
Consuming chips from the box (Gopher loves chips) - we name it as POP operation

Push Operation

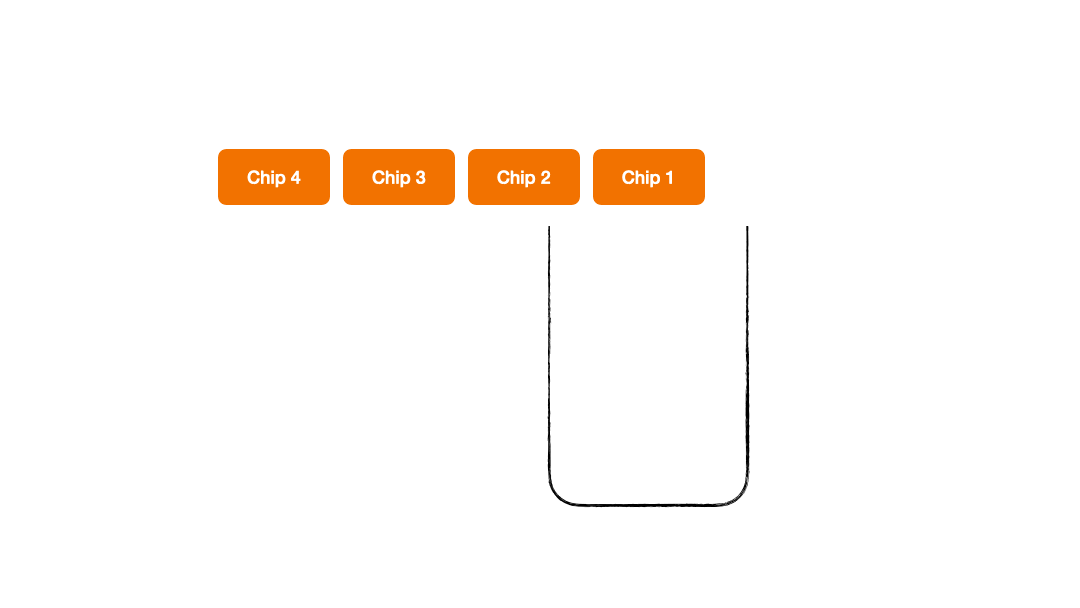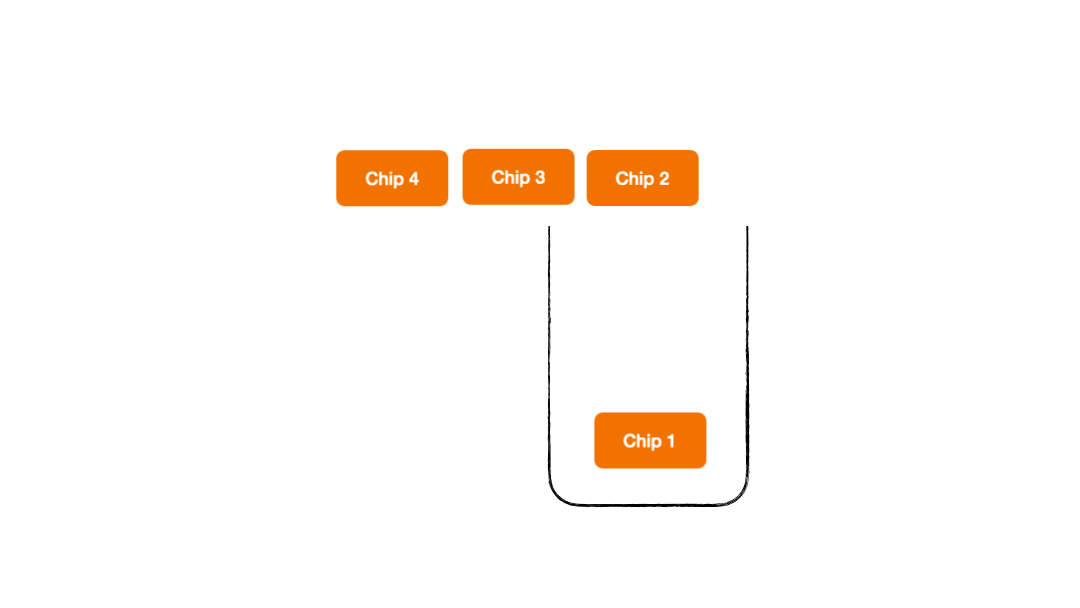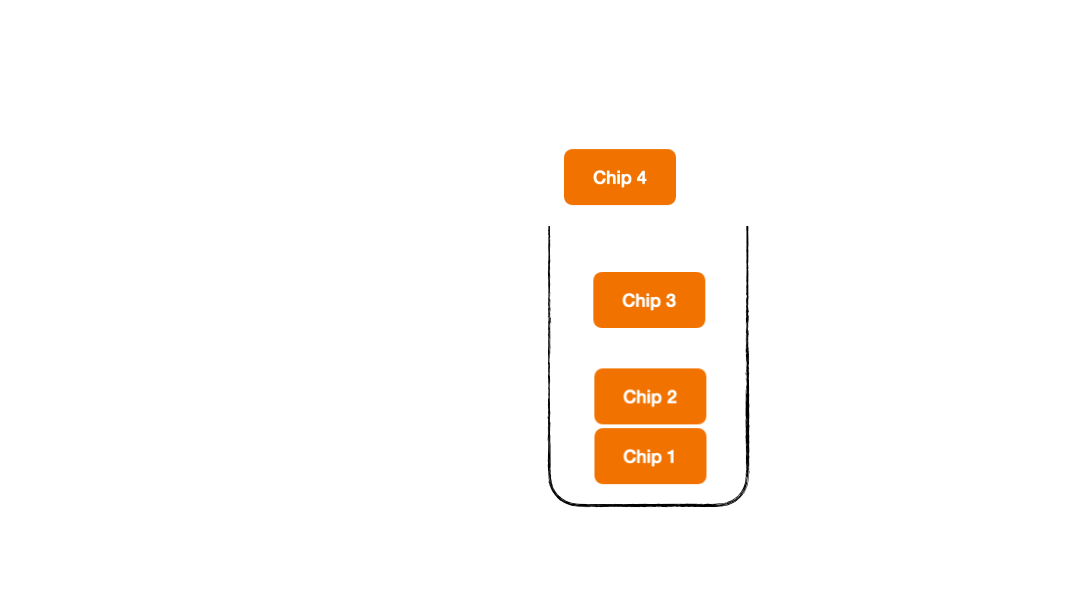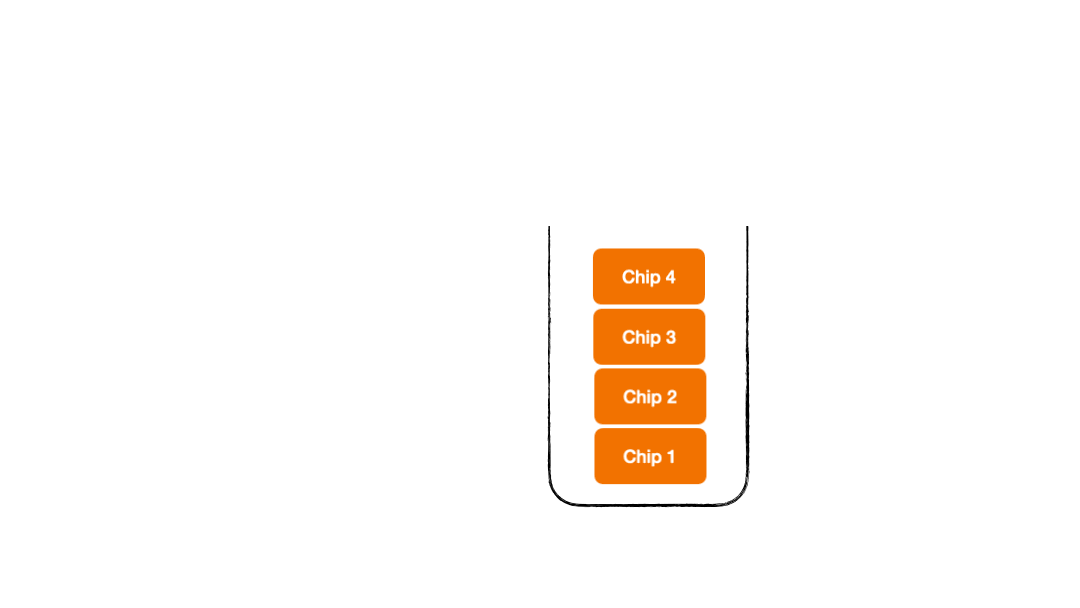
Pop Operation

How would this look like in code ?

Step 1: Understanding the requirement

We need to create a program that will help Gopher enjoy his Stack of chips on a Sunday afternoon watching his favourite show. To do this we need to first create a main.go file(the starting point for all go programs) and import all the necessary packages into it.

Step 2: Package management & type definition

Next let's create a variable which will hold all the values. Imagine this variable as a list which holds all the chip information ,i.e, every chip is essentially a list element. Let's call this list "dataStack".

//Main Package to demostrate Queue data structure
package main

import (
	"container/list"
	"fmt"
)

// In order to group our data we use type - struct
type dataStack struct {
	stack *list.List
}

Step 3: Main function definition

In the previous step we specified how we will store the chip information, now we need to create the same,i.e, initialize the list. We do this at the starting point of every GO program in the main function. We will also invoke all the actions that Gopher will do with the Stack of chips inside this main function.

//Main: Starting point of this GO Program
func main() {
	dataObject := &dataStack{
		stack: list.New(),
	}
	fmt.Printf("Push: Data-1\n")
	dataObject.Push("Data-1")
	fmt.Printf("Push: Data-2\n")
	dataObject.Push("Data-2")
	fmt.Printf("Is Empty: %t\n", dataObject.IsEmpty())
	fmt.Printf("Size: %d\n", dataObject.Size())
	for dataObject.Size() > 0 {
		topVal, _ := dataObject.Peek()
		fmt.Printf("Front: %s\n", topVal)
		fmt.Printf("Pop: %s\n", topVal)
		dataObject.Pop()
	}
	fmt.Printf("Is Empty: %t\n", dataObject.IsEmpty())
	fmt.Printf("Size: %d\n", dataObject.Size())
}

Step 4: Size function definition

At any given point of time, Gopher needs to know the number of chips left in his Stack so that he can order another Stack of chips if needed. To do this we need to create a function called Size(), which returns the size of the Stack at any given point of time

//Size : Return the integer value corresponding to the size of the Stack
func (d *dataStack) Size() int {
	return d.stack.Len()
}

Step 5: Peek function definition

From time to time Gopher likes to take a look at the next chip he is going to eat. Hence we need to create a function called Peek(). The purpose of this function is to return the last chip that was added to the Stack. We use the native list function in GO called "list.Front()" for this purpose as it returns the last chip that was inserted into the list. We should also handle the scenario where the Stack is empty.

// Peek : Return the last Element in the state as per LIFO logic
func (d *dataStack) Peek() (string, error) {
	if d.stack.Len() > 0 {
		if value, ok := d.stack.Front().Value.(string); ok {
			return value, nil
		}
		return "", fmt.Errorf("Peek Error: Stack data type is incorrect")
	}
	return "", fmt.Errorf("Peek Error: Stack is empty")
}

Step 6: Push function Definition

Every time the Stack runs out of chips, Gopher refills the Stack with a new set of chips. In order to perform this action we need to define a PUSH function which will be used to insert chips into the Stack. We will be using the native list function in GO called PushFront() function for this purpose. As the name suggests we simply add an element to the end of the Stack.

// Push : Function to add elements into the stack
func (d *dataStack) Push(value string) {
	d.stack.PushFront(value)
}

Step 7: Pop function definition

Gopher went to all this trouble to watch his favourite show while lounging on his favourite couch eating his favourite stack of chips. In order for Gopher to eat his chips, we need to create a POP function. We will also need to let Gopher know when he runs out of chips so that he can do the needful. Let's take a look at how we will achieve this.

// Pop : Function to remove elements from the stack
func (d *dataStack) Pop() error {
	if d.stack.Len() > 0 {
		element := d.stack.Front()
		d.stack.Remove(element)
	}
	return fmt.Errorf("Pop Error: Stack is Empty")
}

Please find the complete working code for Stack at the following location:

Let's talk performance now!

The only two complexities in terms of performance that we care about is the amount of time Gopher will take to perform any CHIP operation on this Stack (Time Complexity) and the space this Stack of chips takes (Space Complexity).

Time Complexity

Inserting a Chip: Gopher will always be able to add a new chip to the top of the Stack , this is a very easy task. We always take the same amount of time to insert a chip to the top of the Stack. Hence this is termed as Constant Time Complexity and is denoted as O(1).
Removing a Chip: Gopher can only remove a chip from the top of the Stack, this very similar to inserting a chip and for this reason the amount of time taken to remove a chip is again Constant Time Complexity and is denoted as O(1).
Searching for a Chip: Gopher needs to go through the entire Stack of chips if he has to locate a particular chip. This means that if there are N number of chips in a Stack he will have to go through each and every one of these chips to find the chip he is looking for. For this very reason the amount of time taken by Gopher to locate a particular chip is Linear Time Complexity and is denoted as O(N).

Space Complexity

If there are N chips that needs to be stored then we need a Stack of size N. Therefore the Space Complexity for a stack is termed as Linear Space Complexity and is denoted as O(N).

In the next post we will see some real world examples where the concept of stack is used.