What is a Heap?What is the difference between Min Heap and Max Heap?
Remember those school days ?
During school days , you typically start your day by standing in line and reciting the national anthem, school songs and the national pledge. On almost all days this line of students are organised in ascending/descending order of height. Even though this method was a little regressive in nature it was still effective. Believe me when I say this, many a jokes have been made about this, my favourite being "Remember those days when we made kids stand in the decreasing order of their insecurities?". I have to say no student was harmed in the making of this blog.
Gopher was a teacher's pet and this might be attributed to him being stationed at the start of the line. He enjoyed these school assemblies and those widely dreaded march pasts for those select occasions like sports meets, school day etc.
Just like the school assembly line there is a certain data structure which organises its contents on entry & on exit of a data element in ascending/descending order. This makes it a worthy alternative to different sorting algorithms simply because it's faster.
You guessed it right, I am talking about a Binary Heap data structure. Before we dig deeper and understand what a Binary Heap is , let us familiarise ourselves with some basic concepts.
- A Binary Heap is simply a Binary Tree which is complete.
- A Binary Heap is usually represented using an Array.
- A Binary Heap can either be a Max Binary Heap or a Min Binary Heap
- The first element in a Binary Heap is called the Root Node.
- Each element in a Binary Heap is called a Node.
- Each Node can have a maximum of two child nodes.
- A Node can have no child nodes too.
What does a Binary Tree look like ?
Let us refresh our memory of how a Binary Tree looks like by looking at the following image:
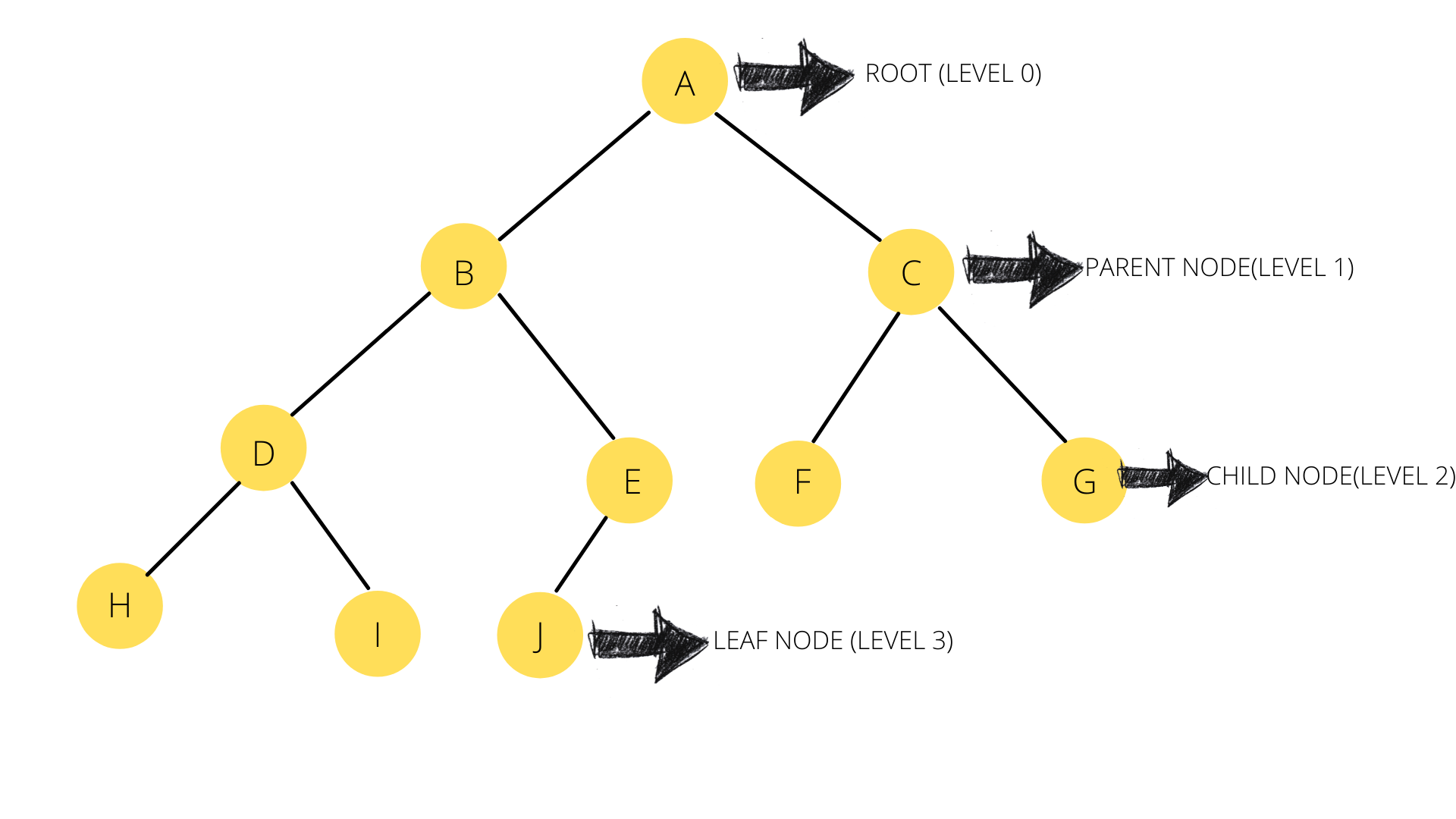
You can go through a more detailed explanation about what a Binary Tree is in our blog about Binary Tree's.
Key Takeways:
- The first node (Level 0) is called a Root Node
- Every node after a Root Node is a Child Node.
- Every Child Node can also be a Parent Node.
- If a Node does not have any children then it is called a Leaf Node.
What is difference between a Max Binary Heap and a Min Binary Heap?
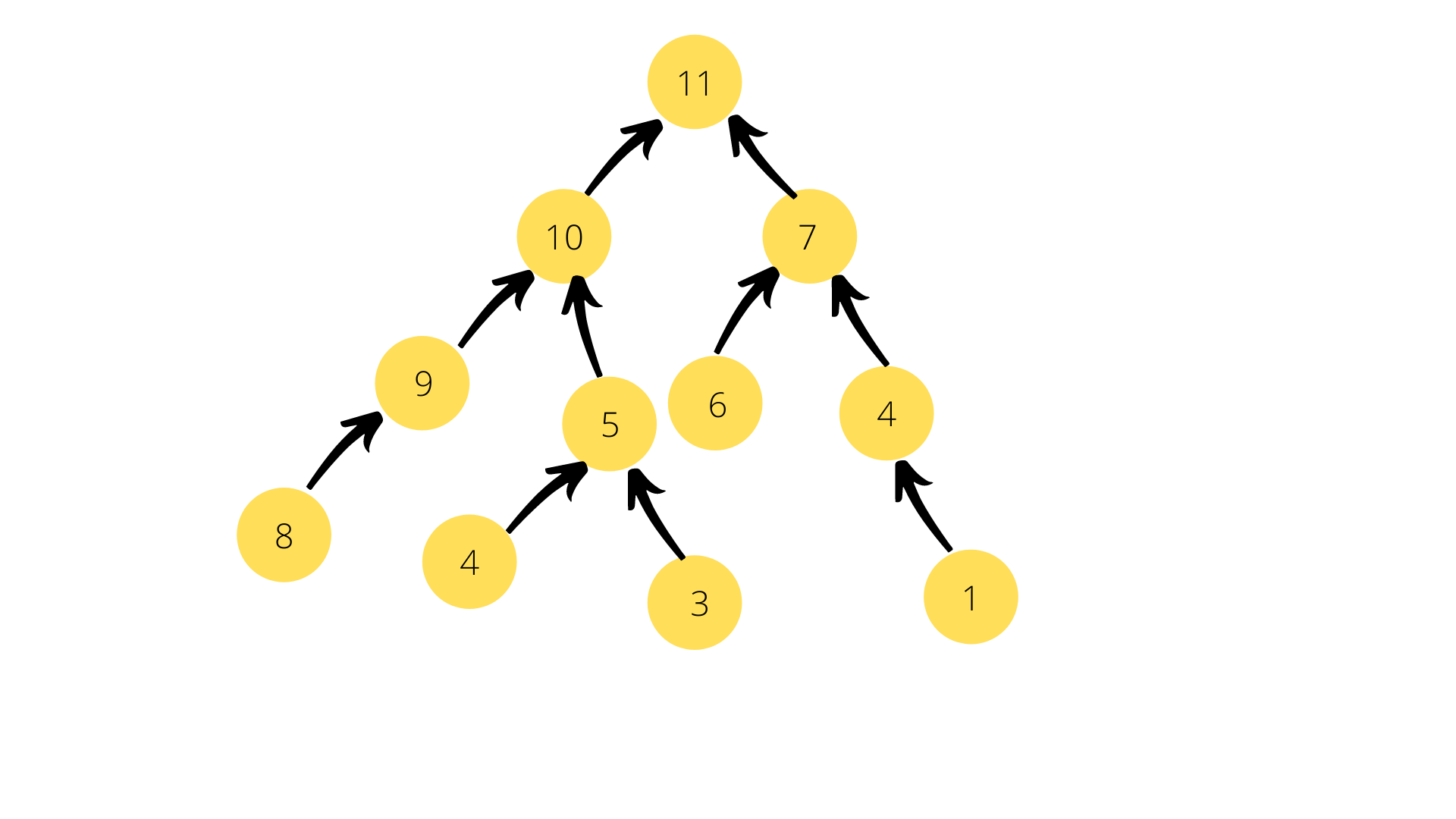
Max Binary Heap
Imagine the school assembly line was arranged in Descending order, this means the tallest person in the class would be standing at the front.
Similarly, in a Max Binary Heap the Root Node holds the maximum value in a given set of data elements. This means that the Array which holds the flattened Max Binary Heap will have the maximum value at the first (Array[0]) position.
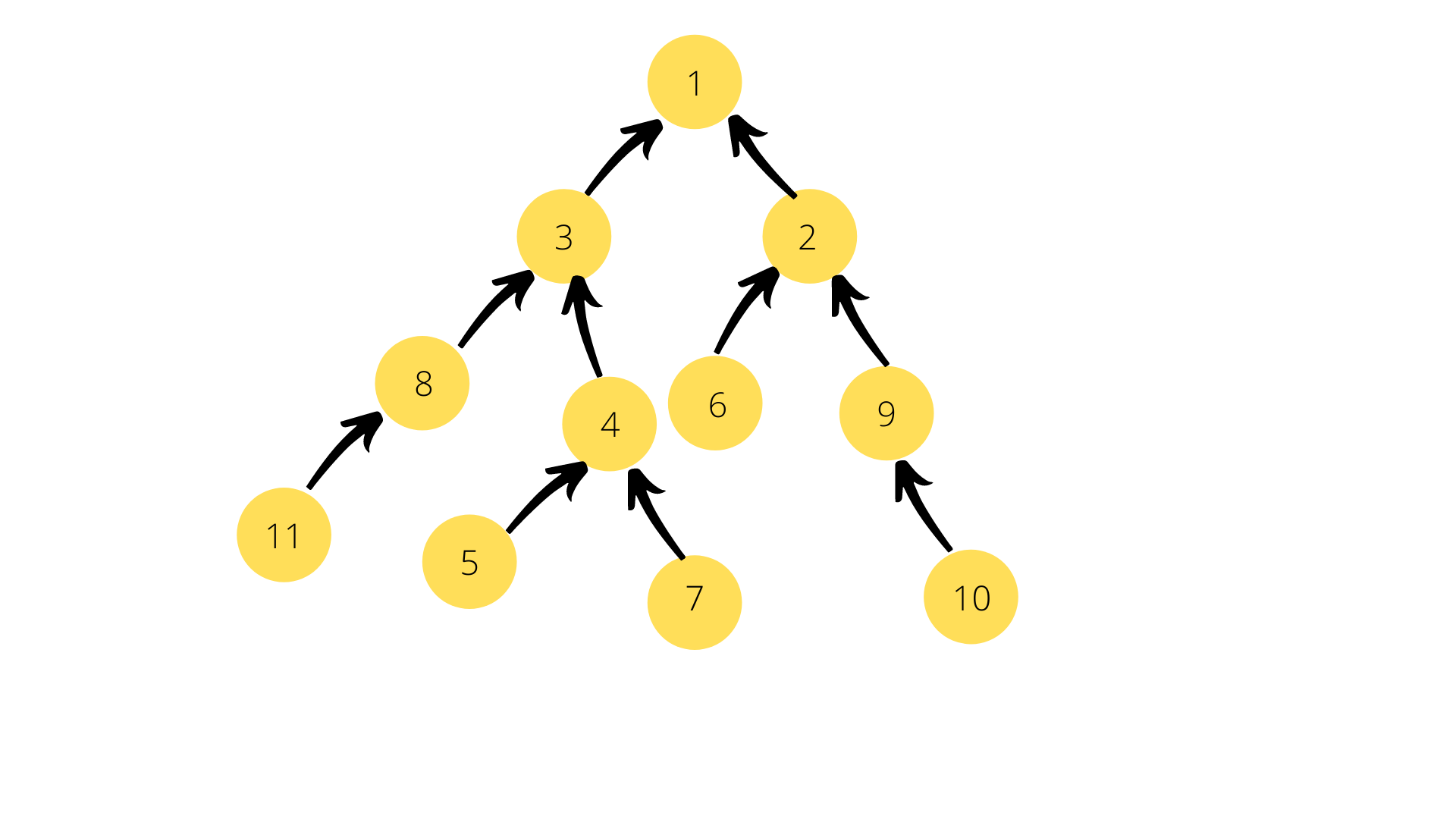
Min Binary Heap
Imagine that the school assembly line was arranged in Ascending order, this means the shortest person in the class would be standing at the front.
Similarly, in a Min Binary Heap the Root Node holds the minimum value in a given set of data elements. This means that the Array which holds the flattened Min Binary Heap will have the minimum value at the first (Array[0]) position.
How is a Heap represented?
As I have mentioned earlier a Heap(Max Binary Heap / Min Binary Heap) can be represented using a 1-Dimensional Array.
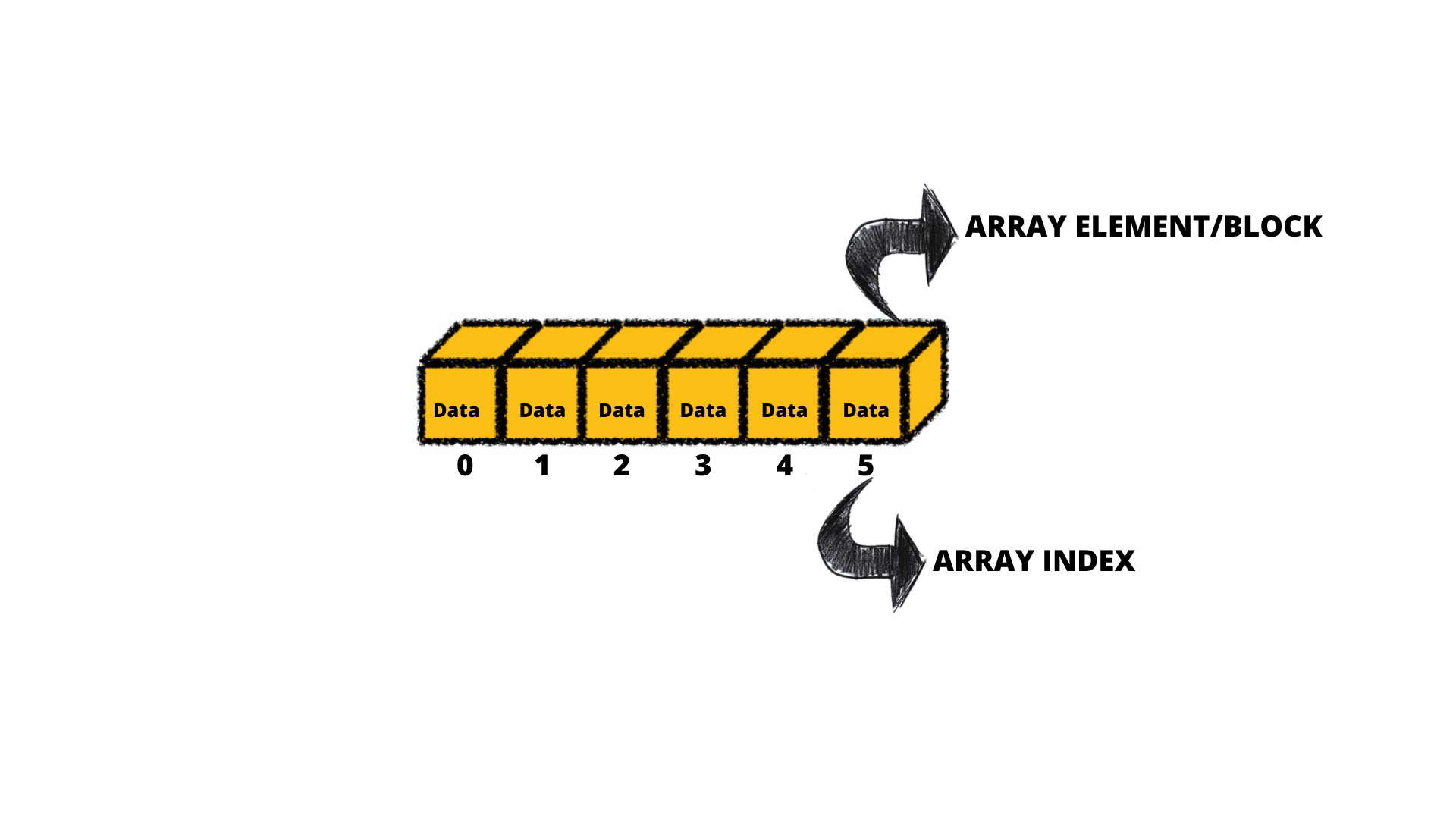
How do we maintain the order in a Heap?
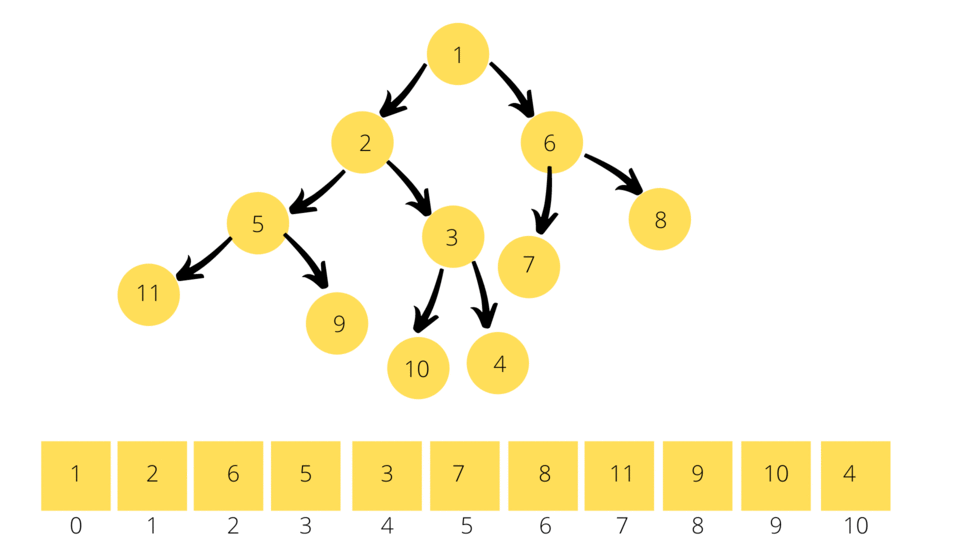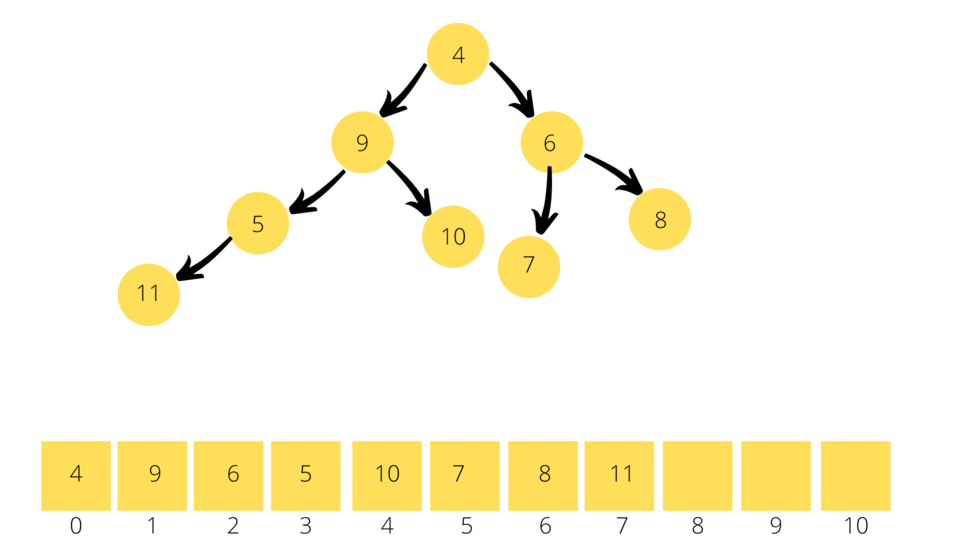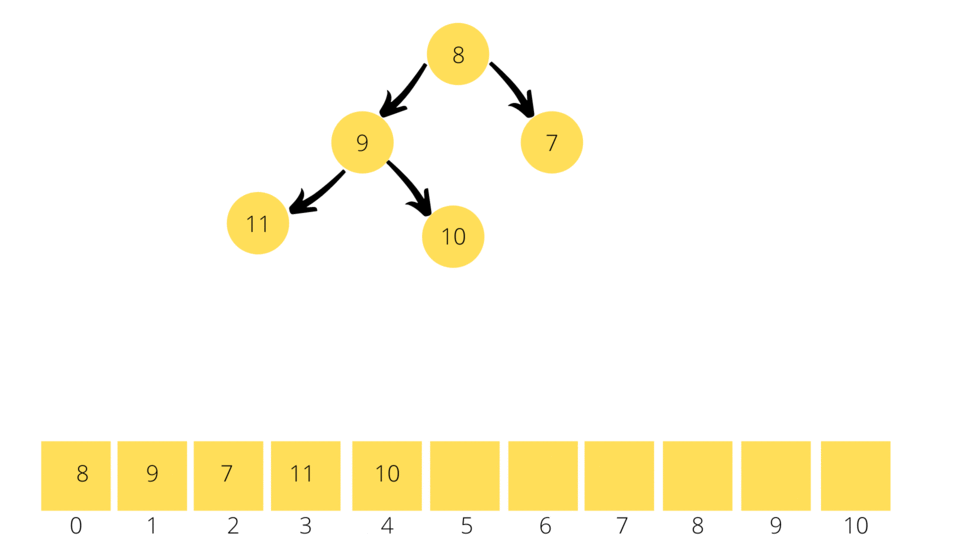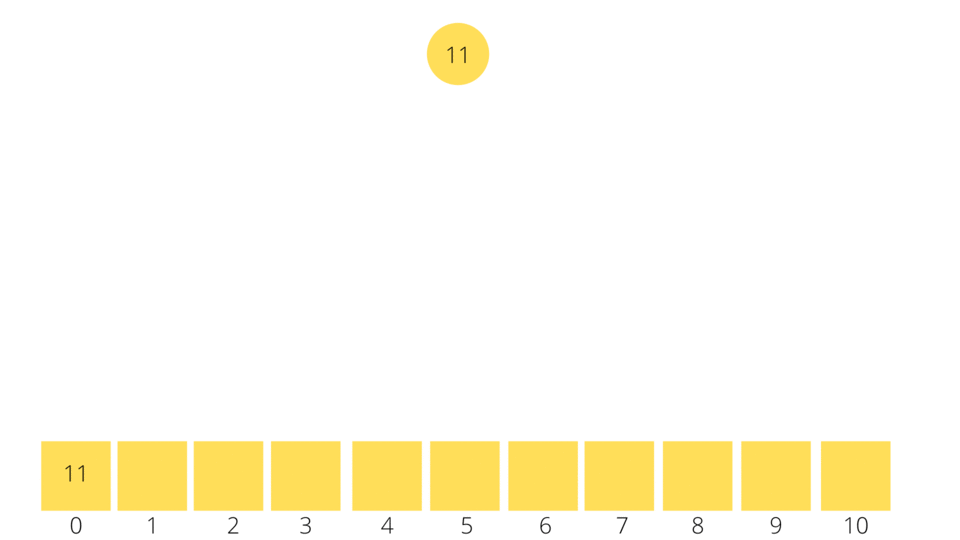
It is only natural to wonder how we can maintain this order of elements even while inserting/deleting elements in to the Heap. Since both Min & Max Binary Heap's are very similar in implementation let us look Min Binary Heap to understand the inner workings of a Heap.
Inserting an element
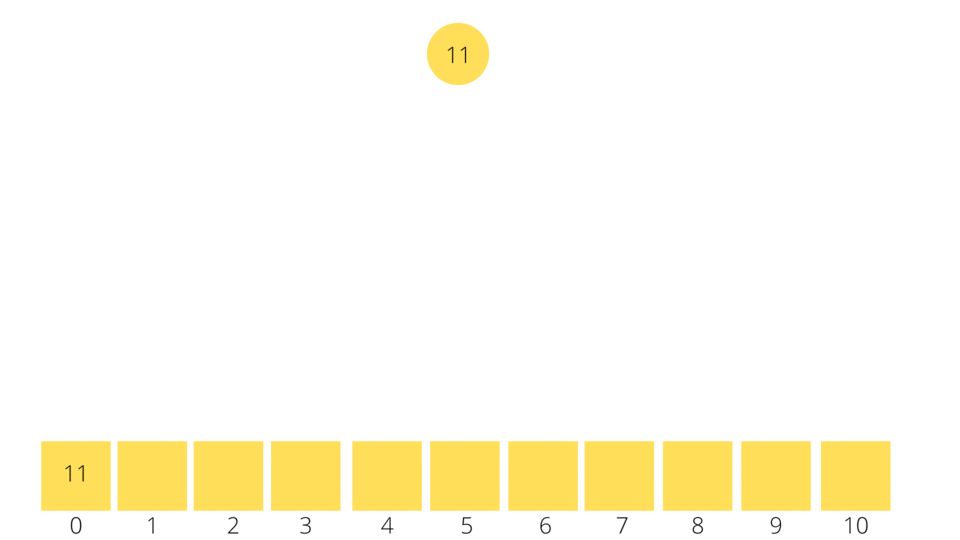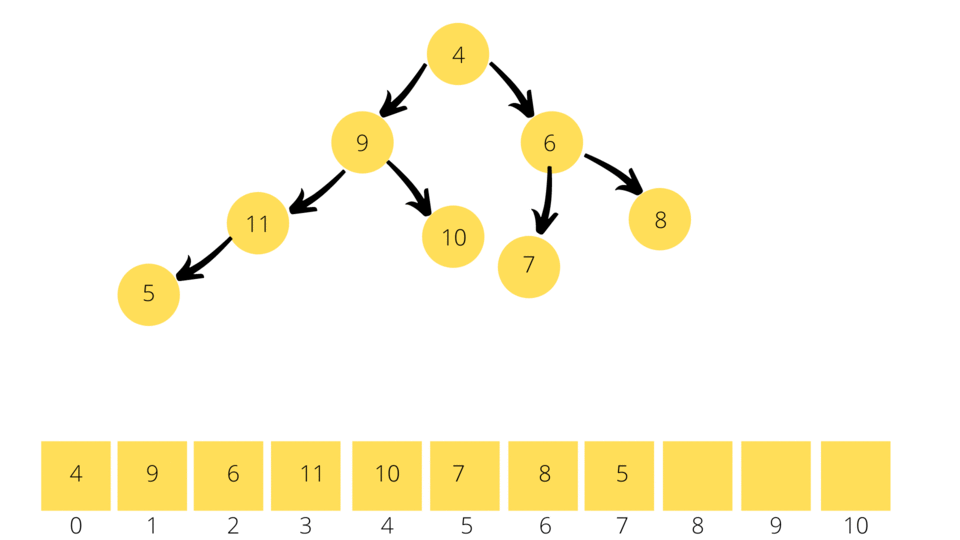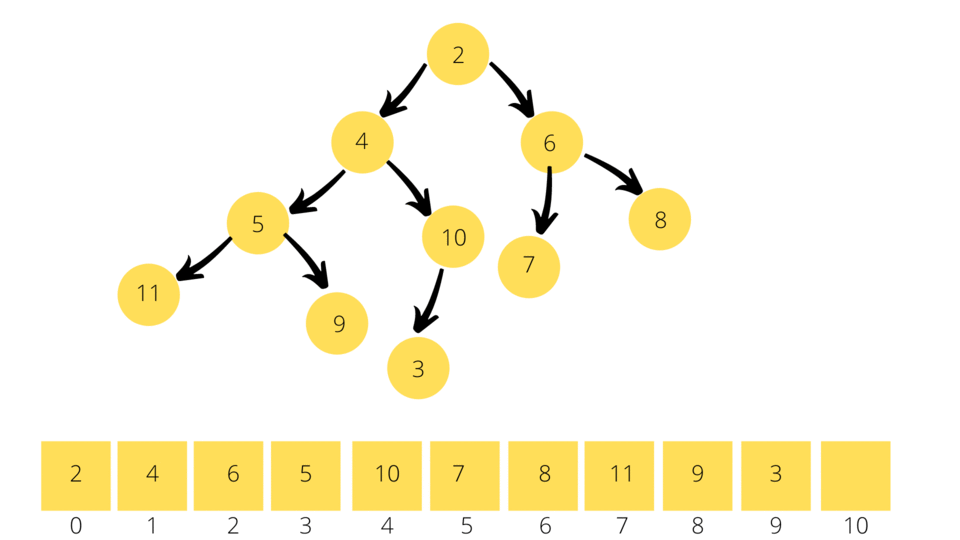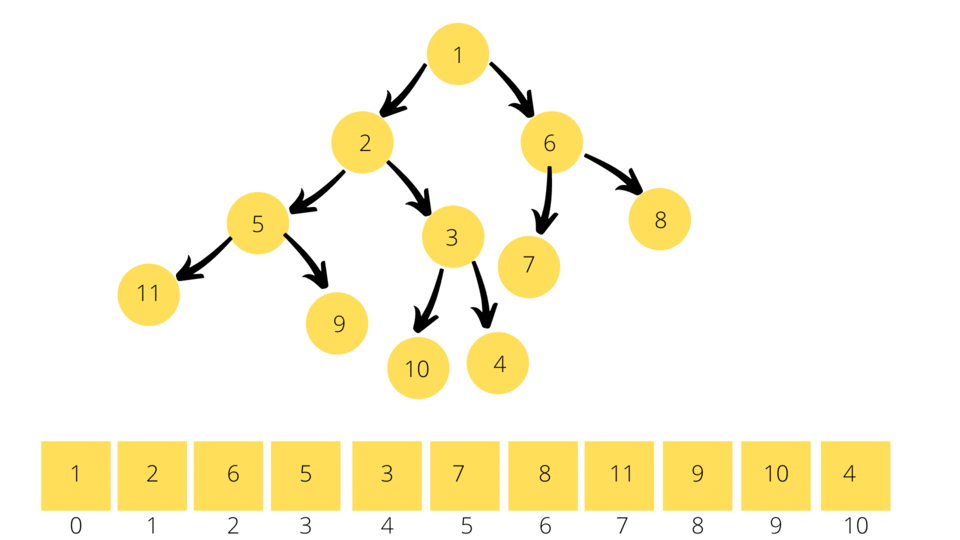
We always insert/append an element to the end of the Binary Heap/Array and then adjust the elements/nodes of the Array/Binary Heap to incorporate the new element. This process is called Bubbling Up. As soon as you append an element to the end of the Min. Binary Heap/Array the data structure tries to find the immediate parent of the inserted element by using the formula:
parentNode = (currentElementPosition - 1)/2.
It then compares the newly inserted element with the parent element , if the parent element is greater than (lesser than in the case of Max Binary Heap) the inserted element then it swaps the two elements. This process is repeated until you reach a parent node which doesn't satisfy the above condition.
Extracting the element with minimum value
As you know the Root Node is the element with the minimum value in a Min Binary Heap, therefore we just have to extract the Root Node at any given point of time to get the minimum value in a Min Binary Heap. Once this happens we need to find a new root node which requires a total reshuffle of the heap. For this purpose, we move the numbers with higher value to the bottom of the heap and the numbers with lower values to the top of the heap. Let's call this process the Bubbling Down Process.
As soon as you remove the Root Node, we take the last element in the Min Binary Heap/Array and substitute it as the new Root Node. We then find the new Child Nodes using the formula:
* Left Child Node = 2 * currentNodePosition + 1
* Right Child Node = 2 * currentNodePosition + 2
Once we know the child nodes we compare the Current Node/Parent Node with each of the child node values. We then swap the nodes if the any of the child node values are lesser than the Parent Node (greater than the Parent Node for Max Binary Heap). This process is continued till all the nodes are in the right positon.
How would this look like in code ?
Step 1: Package Management & type definition
Let us create two variables -
- One will be used to store the integer array and the index in itself ,let us call it Node
- The other will be an integer array, let us call it MinHeap
package main
import (
"fmt"
"time"
"math/rand"
"math"
"strings"
)
type Node struct {
heap *MinHeap
index int
}
type MinHeap struct {
arr []int
}
Step 2: Initialisation
In the previous step, we specified how we will store the information, now we need to figure out a way to create the same,i.e, a function to initialise the Min Binary Heap.
func NewMinHeap(values ...int) *MinHeap {
h := &MinHeap{
arr: append([]int{}, values...),
}
for i := len(h.arr)/2 - 1; i >= 0; i-- {
h.bubbleDown(i)
}
return h
}
Step 3: Insert an Element
Let us now write a function which will be responsible for appending a new element to the Min Binary Heap.
func (h *MinHeap) Insert(value int) {
h.arr = append(h.arr, value)
h.bubbleUp(len(h.arr) - 1)
}
Step 4: Bubble up the new Element
Now that the element has been appended we will need to reshuffle the Heap so that the new element can be moved to the correct position in the Heap.If the element is already in the correct position then we will not rearrange the Heap.
func (h *MinHeap) bubbleUp(idx int) {
for {
parentIdx := (idx - 1) / 2
if idx == 0 || h.arr[parentIdx] <= h.arr[idx] {
break
}
h.arr[idx], h.arr[parentIdx] = h.arr[parentIdx], h.arr[idx]
idx = parentIdx
}
}
Step 5: Remove the element with minimum value
The element with minimum value is the root element.Simply extracting the root element will provide you with the current minimum value.
func (h *MinHeap) extractMin() (int, bool) {
if len(h.arr) == 0 {
return 0, false
}
val := h.arr[0]
h.arr[0], h.arr[len(h.arr)-1] = h.arr[len(h.arr)-1], h.arr[0]
h.arr = h.arr[:len(h.arr)-1]
h.bubbleDown(0)
return val, true
}
Step 6: Perform Bubble Down operation
Once the Root Node is extracted, we need to find a new Root Node/ new minimum value.For this purpose we will be reshuffling the entire Heap again.
func (h *MinHeap) bubbleDown(idx int) {
for {
// pick child to swap (smaller one)
childIdx := idx*2 + 1 // left child
if childIdx >= len(h.arr) || childIdx < 0 { // <0 int overflow
break
}
rightIdx := childIdx + 1
if rightIdx < len(h.arr) && h.arr[childIdx] >= h.arr[rightIdx] {
childIdx = rightIdx
}
// swap
if h.arr[childIdx] >= h.arr[idx] {
break
}
h.arr[idx], h.arr[childIdx] = h.arr[childIdx], h.arr[idx]
idx = childIdx
}
}
Step 7: Print the Heap
In order to print the Heap as we perform various operations on it, we have create a printHeap() method and some auxilliary functions to help with this process.
func (h *MinHeap) PrintHeap() {
for i := 0; i < len(h.arr); i++ {
node := h.nodeAt(i)
// left-side whitespaces
if leftChild := node.LeftChild(); leftChild != nil {
if node.isRightChild() {
fmt.Print(strings.Repeat("-", leftChild.calcPrintWidth()))
} else {
fmt.Print(strings.Repeat(" ", leftChild.calcPrintWidth()))
}
}
// node value
fmt.Printf(" %d ", node.Value())
// right-side whitespaces
if rightChild := node.RightChild(); rightChild != nil {
if i == 0 || node.isRightChild() {
fmt.Print(strings.Repeat(" ", rightChild.calcPrintWidth()))
} else {
fmt.Print(strings.Repeat("-", rightChild.calcPrintWidth()))
}
}
if node.isRightMost() {
if i == len(h.arr)-1 && !node.isRightChild() {
if parent := node.Parent(); parent != nil {
if vw := parent.calcWidth(); vw > 0 {
fmt.Print(strings.Repeat("-", vw/2))
fmt.Print("+")
}
}
}
fmt.Println()
} else {
if rightParent := node.findRightParent(); rightParent != nil {
if vw := rightParent.calcWidth(); vw > 0 {
if node.isRightChild() {
fmt.Print(strings.Repeat(" ", vw))
} else {
fmt.Print(strings.Repeat("-", vw/2))
fmt.Print("+")
fmt.Print(strings.Repeat("-", (vw-1)/2))
}
}
}
}
}
}
Please find the complete working code for Min Binary Heap at the following location:
Let's talk performance now!
The only two complexities in terms of performance that we care about is the time taken to insert/remove a new Node from the Min Binary Heap(Time Complexity) and how big/long the Binary Heap actually is (Space Complexity).
Time Complexity
- Deleting an Element : Since this operation involves returning the Root Node of the Array/Heap and also reshuffling the entire Heap the Time Complexity of this operation is O(log(N)).
- Insert a New Element : Since this operation involves appending the Node to the end of the Array/Heap and then reshffling the entire Heap the Time Complexity of this operation is O(log(N)).
- Extract Minimum Value : Since this operation involves returning the Root Node the Time Complexity of this operation is O(1) .
Space Complexity
If there are N Nodes that needs to be stored then we need a Binary Heap of size N. Therefore the Space Complexity for a Binary Heap is termed as Linear Space Complexity and is denoted as O(N).
Go provides Heap as an in-built package and all of the operations that we discussed in the earlier blog is available for any type that implements the heap interface. You can find more details here: https://pkg.go.dev/container/heap
In the next post we will see some real world examples where the concept of Binary Heap is used.




Join the conversation