Series 2: Queues

What is a Queue? How do I enter values in to a Queue? How do i remove these values?

Have you been to the movies ?

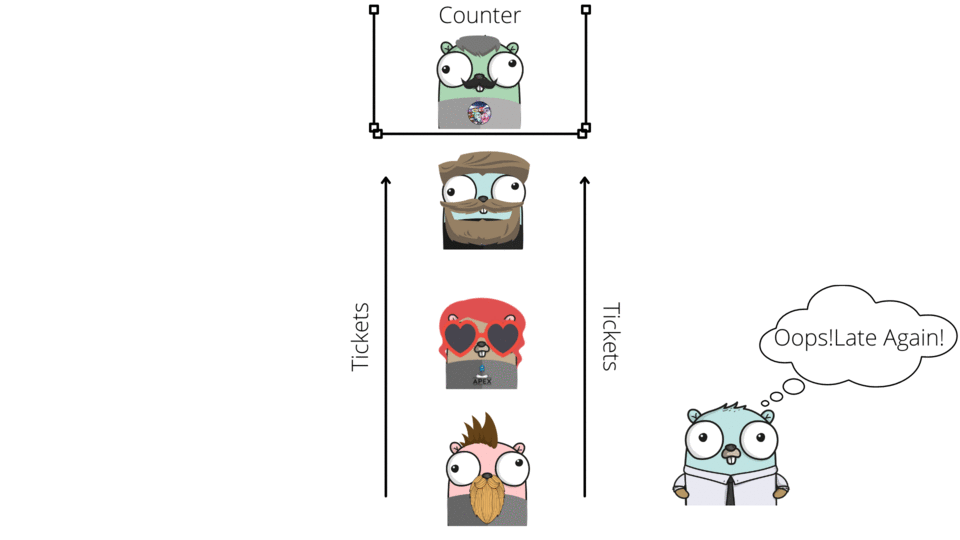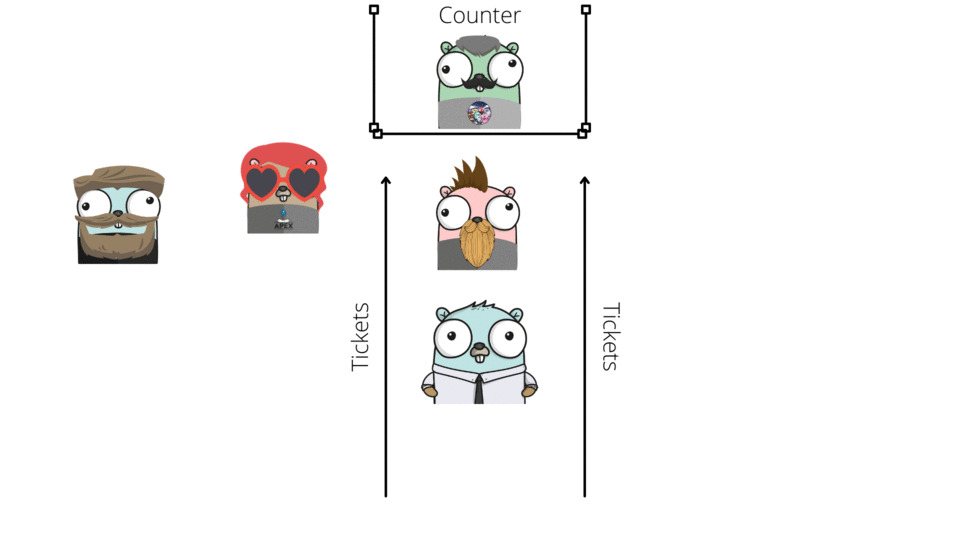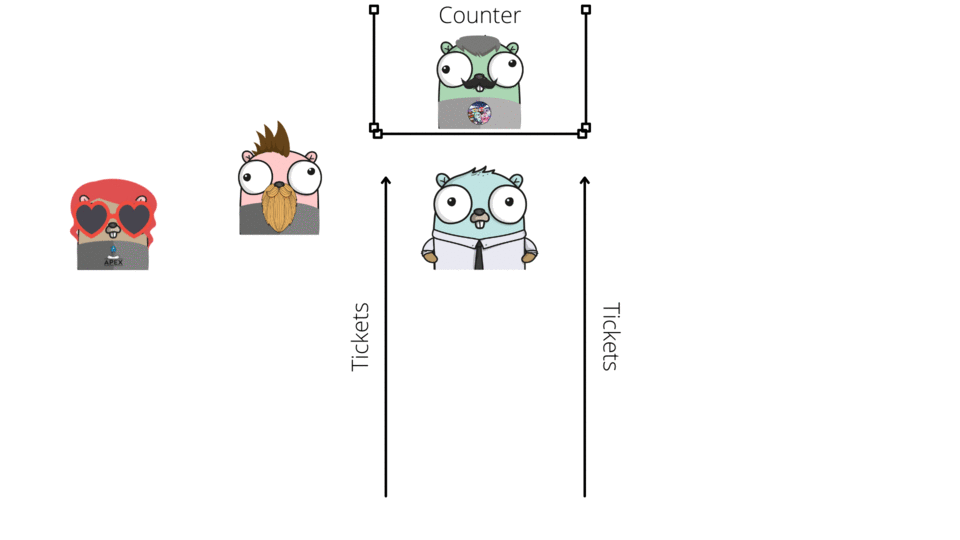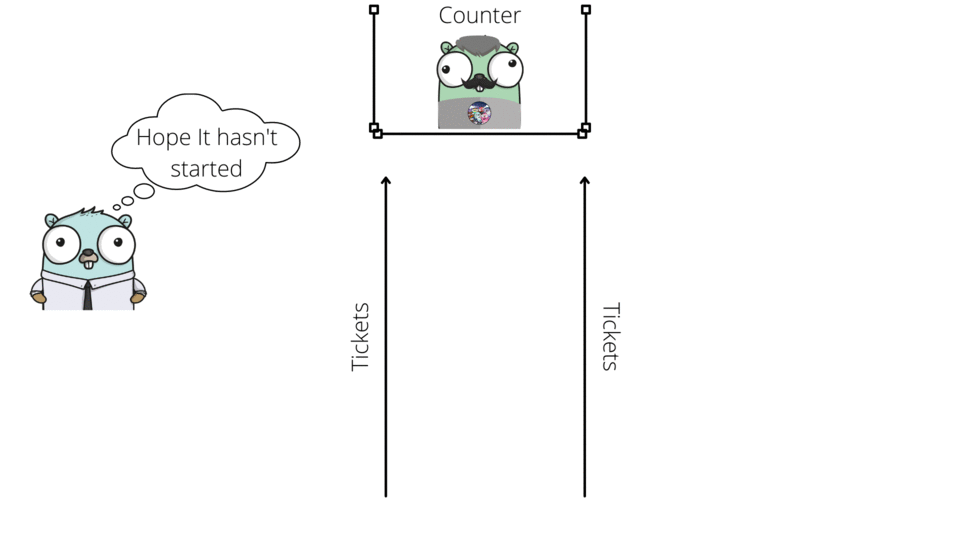
In this episode, we will follow Gopher to the movies.As you all know Gopher by nature is a procrastinator and hence has the habit of doing things at the last minute.Despite numerous reminders from his friends, Gopher reached the movies at the last minute which meant that he ended up at the end of a long QUEUE to buy tickets.

Noticed something peculiar here ? All movie goers stood one behind another to collect their tickets and then exited the Queue from the front of it.

What goes inside in this case comes out first.This is also know as FIFO (First In First Out).The first person who stood in the Queue is also the first person who will be able to purchase the ticket.

What is the definition of a Queue?

A Queue is an abstract data structure which serves as a collection of elements on which any operation can only performed in the order FIFO (First In First Out).

Keeping the above definition as a mental model, let us define some actions which are critical to this data structure.

There are 2 actions that are key to this concept:

1. Entering the Queue - let's call it ENQUEUE operation

2. Exiting the Queue - let's call it DEQUEUE operation

ENQUEUE Operation

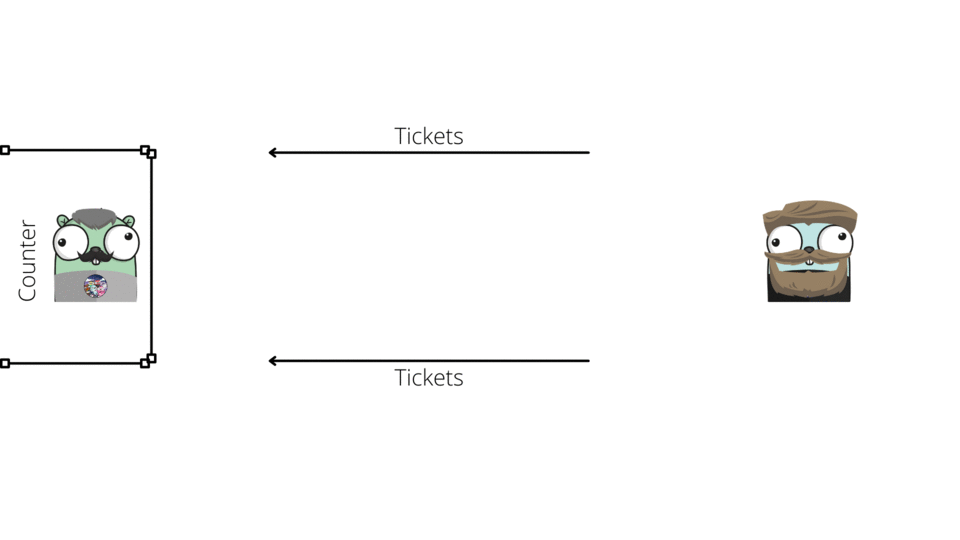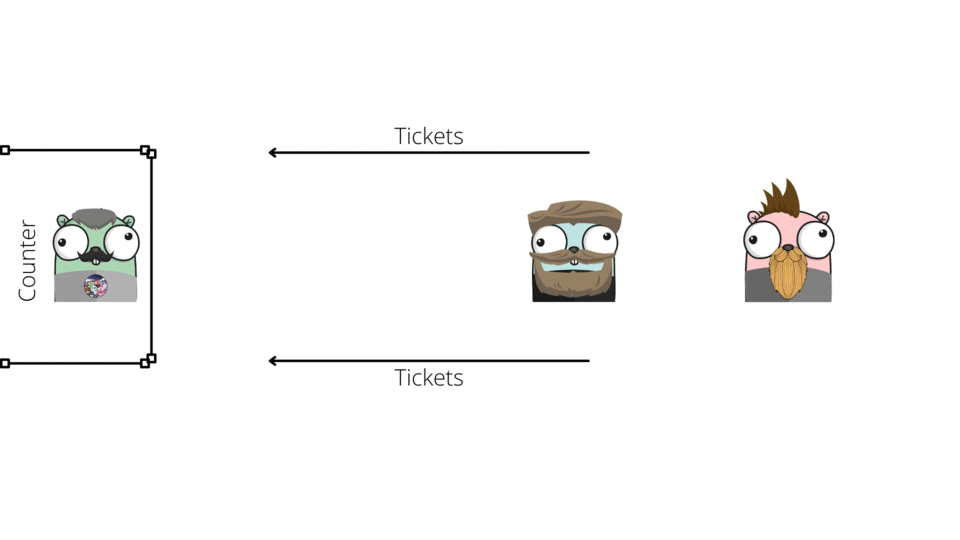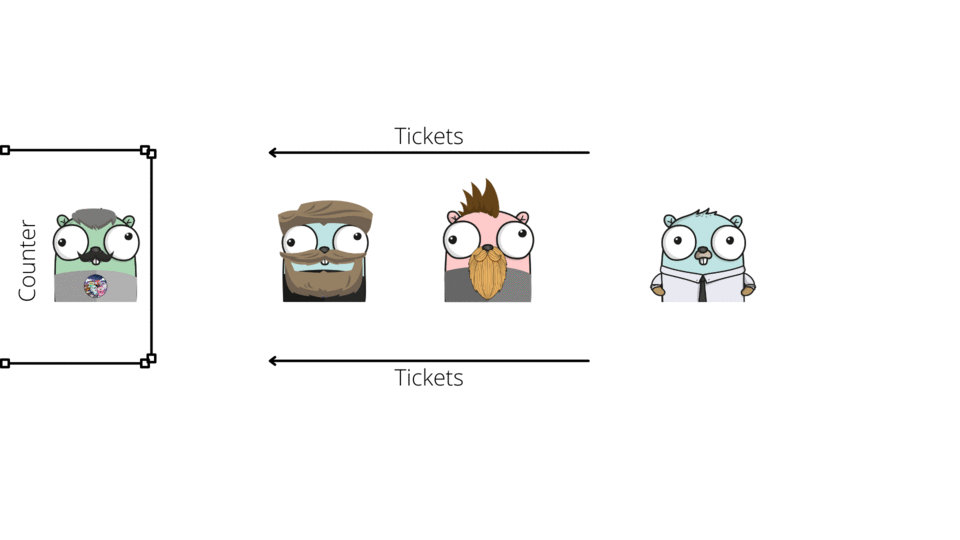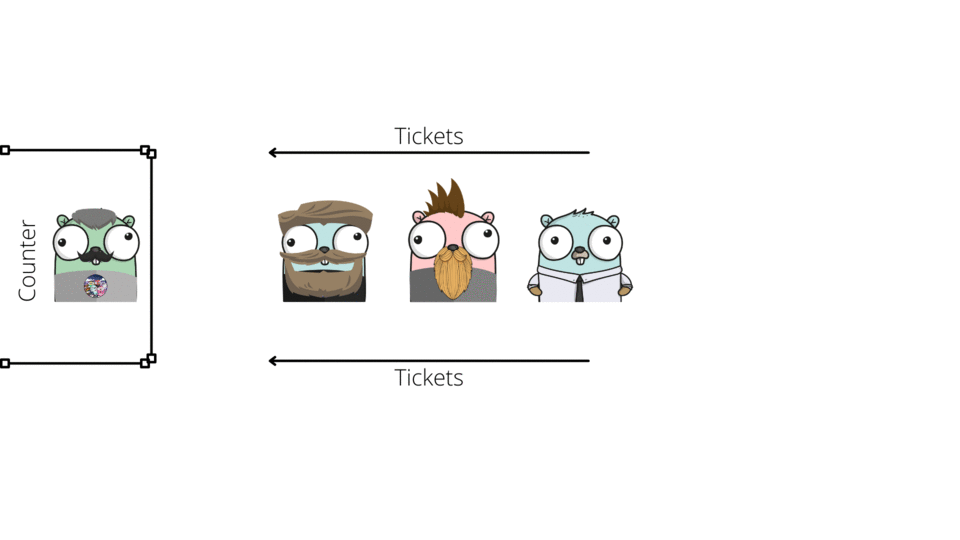
DEQUEUE Operation

How would this look like in code ?

Step 1: Understanding the requirement

The task at hand is to create a program that will get Gopher to watch the new Star Wars movie on opening day.To do this we need to first create a main.go file(which is the starting point for all GO programs) and import all the necessary packages into it.

Step 2: Package management & type definition

Next let us create a variable which will hold all the values.Imagine this variable as an array which represents the individuals standing in Queue to collect their movie tickets ,i.e, every individual is essentially an array element.Let us call this array "queue".

//Main Package to demostrate Queue data structure
package main

import "fmt"

//In order to group our data we use type - struct
type queue struct {
	data []int
}

Step 3: Initialisation

In the previous step, we specified how we will store the information, now we need to figure out a way to create the same ,i.e, a function to initialise the array.

// Function for intializing an instance of Queue struct
func New() *queue {
	return &queue{
		data: []int{},
	}
}

Step 4: Main function definition

The actual initialisation of all the variables happens as always in the main function as it is the starting point for any GO program .Let us go ahead and create one for this program too.

// Main Function
func main() {
	queue := New()
	result, _ := queue.Enqueue(1).Enqueue(2).Enqueue(3).Peek()
	fmt.Println(result)
	fmt.Println(queue.IsEmpty())
	result, _ = queue.Dequeue()
	fmt.Println(result)
	result, _ = queue.Dequeue()
	fmt.Println(result)
	result = queue.Size()
	fmt.Println("Size is: ",result)
	queue.Dequeue()
	fmt.Println(queue.IsEmpty())
	_, err := queue.Peek()
	fmt.Println(err)
}

Step 5: Size function definition

At any point of time Gopher would likes to know the amount of time he has to wait to get the tickets.To do this we need to create a function called Size(), which returns the size of the Queue at any given point of time.

// Size : Return the size of the array.
func (q *queue) Size() int {
	return len(q.data)
}

Step 6: isEmpty function definition

At any point of time Gopher would like to know if the Queue is empty.To do this we need to create a function called isEmpty(), which returns a boolean.

// Function to check if the queue data structure is empty
func (q *queue) IsEmpty() bool {
	return len(q.data) == 0
}

Step 7: Peek function definition

From time to time Gopher would also like to take a look at who is currently at the counter to judge the amount of tickets left for the show.Hence we need to create a function called Peek().The purpose of this function is to return the first element that entered the Queue.

// Peek : Return the first Element in the queue as per FIFO logic
func (q *queue) Peek() (int, error) {
	if len(q.data) == 0 {
		return 0, fmt.Errorf("Queue is empty.Please add elements")
	}
	return q.data[0], nil
}

Step 8: Enqueue function definition

In order to collect his tickets Gopher has to join the queue.In order to perform this action in our program let us define an ENQUEUE function which will insert Gopher at the end of the Queue.

// Enqueue : Function to add elements into the Queue
func (q *queue) Enqueue(n int) *queue {
	q.data = append(q.data, n)
	return q
}

Step 9: Dequeue function definition

Once Gopher reaches the front of the Queue at the counter he can collect the ticket and exit the Queue so that he can go to the movie hall to find his seat and watch his movie finally with some cheese popcorn.In our program we can achieve this by creating a DEQUEUE function which will remove the first element at the front of the Queue.

// Dequeue : Function to remove elements from the Queue
func (q *queue) Dequeue() (int, error) {
	if len(q.data) == 0 {
		return 0, fmt.Errorf("Queue is empty.Please add elements")
	}
	element := q.data[0]
	q.data = q.data[1:]
	return element, nil
}

Please find the complete working code for Queue at the following location:

Let's talk performance now!

The only two complexities in terms of performance that we care about is the amount of time Gopher will take to purchase his movie tickets by standing in Queue(Time Complexity) and how big/long the Queue actually is (Space Complexity).

Time Complexity

Entering the Queue: Gopher will always be able to join the Queue at the back , this is a very easy task. We always take the same amount of time to join the Queue at the back. Hence this is termed as Constant Time Complexity and is denoted as O(1).
Exiting the Queue: Gopher can only exit the Queue from it's front, this is very similar to entering the Queue and for this reason the amount of time taken to exit the queue is again Constant Time Complexity and is denoted as O(1).
Searching for a Friend in Queue: Gopher needs to go through the entire Queue of individuals if he has to locate a friend. This means that if there are N number of individuals in a Queue he will have to go through each and every one of them to find his friend. For this very reason the amount of time taken by Gopher to locate a friend is Linear Time Complexity and is denoted as O(N).

Space Complexity

If there are N individuals that needs to be stored then we need a Queue of size N. Therefore the Space Complexity for a Queue is termed as Linear Space Complexity and is denoted as O(N).

In the next post we will see some real world examples where the concept of Queue is used.